How to power a 12 volt LED?

I need to go to turn on a LED from a voltage of 12V …

What circuit should I make?

It is simple.

The LED must be supplied with a voltage of 1.5 V, and 20mA must flow through it (if it is not blinking, otherwise 15mA). To lower the voltage to 12V, you need to put a resistor in series with the LED to 12 – 1.5 = 10.5V.

You also need to ensure that the resistor (which is in series with the LED and therefore draws the same current) is sized to pull precisely the current that the LED needs to attract.

So from Ohm’s law, we get R = V / I = 10.5 / 0.02 = 525 ohms.

For the power delivered by the resistor, you need to use the power formula P=V*I =10.5*0.02=0.21W, so a 1/4 watt resistor would be sufficient. Still, given the negligible cost difference, I would choose a 1/2 watt resistor.

PS. around a 20ma 12volt led, an 860ohm 1/4w resistor is enough… I have driven a lot of LEDs this way ^_^.

like this: (+12)——–(RRRR)——–(+LED-)—–(GND)

RRR=resistor

+LED- = LED each with anode (+) and cathode (-)

You can recognize the anode by the fact that it is the most extended pin.

How can I connect a 3 volt LED to a 12-volt battery?

If I understand you correctly, your question refers to a 12 V powered relay that, when it closes, discharges a 400 V charged capacitor with a capacitance of 3.3 millifarads.

The first observation is that the capacitance is very high.

The second is that a limiting resistor must be placed. Otherwise, a very high current will flow through the ordinarily low resistance conductor.

If I understood you correctly, the charge of the capacitor is calculated from the basic formula Q=CV=0.003F400V. Remembering that the farad is dimensionally equivalent to one coulomb per volt, we have that the capacitor’s charge is Q=0.003∗400=1.2 coulombs.

Suppose we have a 10 amp 400-volt relay. That is, it can carry a current of 10 amps at a maximum voltage of 400 volts.

Recall that the current charge is divided by the discharge time, so if I=Q/t, t=Q/I=1.2/10=0.12 seconds. That is, if we can discharge the capacitor in a little more than a second, then we are (on average) below the current value (10A) that our relay can conduct without breaking.

Then it is necessary to determine a resistance so that the discharge time is equal to 0.12 seconds. Suppose we remember that the discharge (or charge) time of a capacitor is similar to 5RC. In that case, i.e., 99.9% of the charge is discharged five times the product of the discharge resistance and the capacitance (Discharge of a capacitor – Wikipedia), it follows that 5RC=0.12s R=0.12s5C=0.12s50.003F=8 Ohms.

This is a simple calculation and, therefore, approximate.

The approximation comes from the fact that I took the average current throughout the discharge to be ten amps, but realistically the initial value is much higher.

I simulated a trivial circuit to get an idea of what happens, and I used Qucs (Quite Universal Circuit Simulator), a simulator widely used in the Linux world. —P1

Instead of simulating a relay, I considered a 100V pulse. I used 100V because the simulator has a problem with convection at 400V, but multiply the current by four.

As you can see (graph on the right), the peak current is over 40 amps. The average current is much lower, but the peak current, which usually occurs during transients, is much higher.

If you increase the discharge resistance to 40 ohms, the following happens

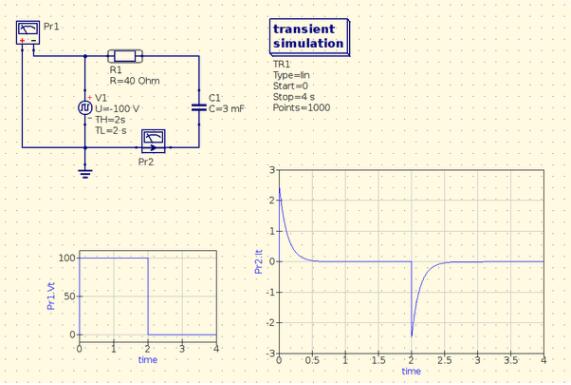
The peak current has dropped to 10 amps (remember you have to multiply the scale by four), and obviously, the discharge time has increased.

So I suggest a 40-ohm resistor, although I would increase it a bit to be on the safe side.

One final consideration is the energy of the discharge.

The energy contained in this mega-capacitor when charged is 12CV2=0.5×0.003×4002=240 joules. Since the discharge takes about half a second, there is about 480 W (half a kilowatt) circulating in this resistor, so you have to take a power resistor and possibly dissipate it as well, or you run the risk of melting it.

ADDENDUM

BTW, I don’t even know if you can find a 3.3 millifarad capacitor on the market that will work at 400V.

At millifarad values, the maximum voltages are 25 volts. The reason is simple: they are electrolytic capacitors, where the two armatures are created by chemical attack and oxidation of an aluminum strip, so the dielectric strength of the material is low: if you apply a voltage to a 25 V capacitor that is even 20% higher than this, the life is significantly reduced.

the life is reduced if it does not burst in your hand (electrolytes have a safety valve: you hear a whistle, and a smell of burnt chicken spreads)

If it survives, it heats up and has very high leakage currents. It probably only lasts a short time.

The resistor in series with the LED is placed to limit the current it will draw or burn out immediately.

To calculate what resistor to put there, do the calculation using Ohm’s law based on three essential pieces of data:

– The input voltage, which in this case is 12V.

The nominal voltage of the LED itself, a parameter set for each LED up to down, then depends on the type: whether high brightness or normal.

– The maximum mA that you want to pass in the LED.

The 12V we have them, as mA absorption is good to 10 or max to 20 if you burn one to the next you set.

For the nominal voltage, say 3V, but you could also reach 4V if they have high brightness.

Now apply the formula:

R= (input voltage – nominal voltage) / mA (in the formula, you have to write it as A, but that means if it’s ten mA, put 0.01A….if it’s 20 mA, it’s 0.02A, and so on)

like this:

R= (12 – 4 “depending on the type of LED as mentioned above”) / 0.02A = 400 ohms.

Since 400 ohms is not a value, you can find on the market, put in the value closest to that value, for example, 390 or 470 ohms.

Or do as I do, that I put 470 ohms to all the default values and play it safe.

If you want to try, set a random resistor, but not too low, and vary it until you get the Lumosota ‘you want.

If you want to be cool, you can put a potentiometer so you can vary the luminosity.

If you want to be cool, look at the maximum current that can support the LED and put the resistor in series with the potentiometer that competes, doing the calculations you suggested so you do not risk burning out the LED.

How to power a 12 volt LED?

Getting a resistor value to insert into a series with one or more LEDs is a reasonably straightforward process.

Need to know some technical characteristics, such as the supply voltage of the circuit; the voltage that will fall on each LED; the current that will flow in the LED, and then by Ohm’s law with a simple step, you will obtain the final value of the resistor to be inserted in series in the circuit.

Main formulas of Ohm’s law:

Legend:

You can use these simple formulas to size your circuit, but in this case, let’s see how to get the value of the resistor shown in the figure above.

You can see that the supply voltage is 12 V, and the LEDs are connected in series 2.

Of course, we can find all the exact characteristics of LEDs on their respective datasheets, but we will use a classic LED diode for the calculation.

Since we know that LED diodes work with a voltage of 2.5 V and a current between 10 and 30 mA (the more you increase the current flowing through the LED diode, the shorter the life of the LED), we will limit ourselves to a current of 15 mA in this example.

Since we know that two LEDs are connected in series, and the voltage drop across each LED is 2.5 V, we deduce that the voltage the resistor must contain will be as follows:

12 – (2.5 * 2)= 7 volts.

We will then use this formula:

R = V: A, where V is equal to 7, while A is similar to 0.015A (to convert the value of mA to A, we must divide the value by 1000)

R1 = 7 : 0.015 = 466 OHM

The value 466 ohms is then the resistor value inserted in series with the circuit to limit the current to 15 mA. However, since this is not a traditional value, we will use the next value, 470 ohms (check the deals).

Last, calculate the power of the resistor.

W=V*A

where V equals 7, while A equals 0.015A

W=7*0.015=0.105 W

In this case, a classic resistor of 1/4 watt is sufficient.